복합체 패턴

제품군과 상자군이라는 두 가지 유형의 객체가 있을 때 상자에는 여러 개의 제품군과 여러 개의 작은 상자군이 포함될 수 있다. 상자군 또한 제품군 또는 더 작은 상자군을 담을 수 있다.

이러한 시스템을 만든다고 가정할 때 총 가격은 어떻게 계산할 것인가? 직접 모든 상자에 접근해서 가격의 합계를 계산하는 방법도 있지만 루프문으로 해결하기는 쉽지않다. 왜냐면 모든 상자 및 제품의 내용을 알고 있어야하기 때문이다.

해결

복합체 패턴은 총가격을 계산하는 메서드를 선언하는 공통 인터페이스를 통해 제품군과 상자군 클래스들과 작업한다. 이 메소드는 단순히 제품 가격을 반환한다. 상자 내부 구성요소의 모든 가격이 계산될 때까지 내용물을 살펴볼 수 있다. 이점은 더 이상 트리를 구성하는 객체들의 구상 클래스들에 대해 신경 쓸 필요도 또 물건이 단순한 제품인지 내용물이 있는 상자인지 알 필요도 없다는 점이다.

구조

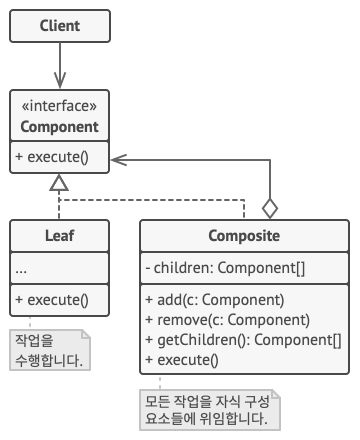
• 컴포넌트 인터페이스는 트리의 단순 요소들과 복잡한 요소들 모두에 공통적인 작업을 설명한다.
• 잎은 트리의 기본 요소이며 하위요소가 없습니다.
• 컨테이너는 하위 요소들이 있는 요소이다. 컨테이너는 자녀들의 구상 클래스들을 알지 못하고, 컴포넌트 인터페이스를 통해서만 모든 하위요소들과 함께 작동한다.
• 클라이언트는 컴포넌트 인터페이스를 통해 모든 요소들과 작동한다. 그 결과 클라이언트는 트리의 단순 요소들 또는 복잡한 요소들 모두에 대해 같은 방식으로 작업할 수 있다.

interface Graphic {
  fun move(x, y)
  
  fun draw()
}

open class Dot : Graphic {
  var x: Int
  var y: Int
  
  override fun move(val x: Int, val y: Int): void {
    this.x += x
    this.y += y
  }
  
  override fun draw() {
    TODO()
  }
}

class Circle : Dot(x, y) {
  var radius: Float
  
  fun draw() {
    TODO()
  }
}

class CompoundGraphic : Graphic {
  val children: List<Graphic>
  
  fun add(child: Graphic) {
    children.add(child)
  }
  
  override fun move(val x: Int, val y: Int) {
    children.forEach {
      child -> child.move(x, y)
    }
  }
  
  fun draw()
}

적용

• 트리구조에 적합하다
• 이 패턴은 클라이언트 코드가 단순 요소들과 복합 요소들을 모두 균일하게 처리하고 싶을 때 사용한다

장단점

• 다형성과 재귀를 사용해 복잡한 트리 구조를 편리하게 작업할 수 있다
• 개방/폐쇄 원칙을 준수한다
• 기능이 다른 클래들은 공통 인터페이스를 제공하기 어려울 수 있다.